非心t分布

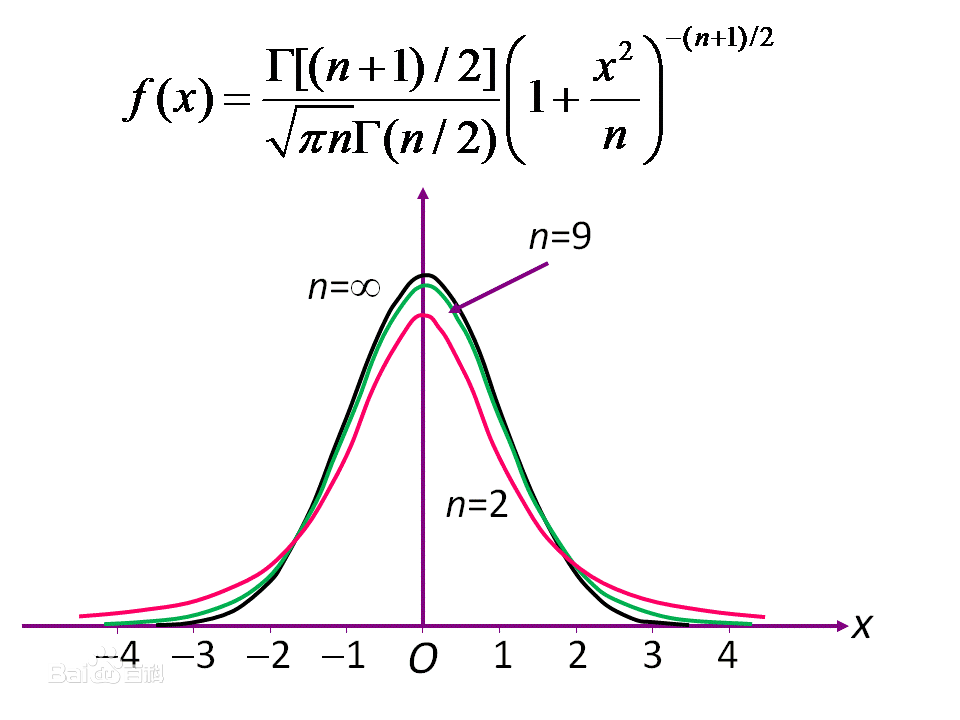
非心t分布（ひしんティーぶんぷ、英: noncentric t-distribution）とは、確率分布と統計学におけるスチューデントのt分布を一般化したものである。

非心な統計母数、例えば「X の上位10パーセント値」のようなものの信頼区間を標本データだけに基いて計算するのに有用である。

非心t分布の特徴

Z は分散 1、平均 0 の正規分布 に従う確率変数 、V は自由度 νのカイ二乗分布に従いかつ、Z と独立な確率変数、μは実定数としたときに、

${\displaystyle T={\frac {Z \mu }{\sqrt {V/\nu }}}}$

が従う分布のことを「自由度ν、非心パラメーターμの非心t分布」と呼ぶ。μ=0の場合はt分布そのものである。この非心t分布においては（非心F分布等の他の多くの非心分布とは異なり）非心パラメータμは負の値であってもよい。

累積分布関数

この非心t分布の累積分布関数は、以下の式で与えられる。

${\displaystyle F_{\nu ,\mu }(x)={\begin{cases}{\tilde {F}}_{\nu ,\mu }(x),&{\mbox{if }}x\geq 0;\\1-{\tilde {F}}_{\nu ,-\mu }(x),&{\mbox{if }}x<0,\end{cases}}}$

ここで、

${\displaystyle {\tilde {F}}_{\nu ,\mu }(x)=\Phi (-\mu ) {\frac {1}{2}}\sum _{j=0}^{\infty }\left[p_{j}I_{y}\left(j {\frac {1}{2}},{\frac {\nu }{2}}\right) q_{j}I_{y}\left(j 1,{\frac {\nu }{2}}\right)\right],}$

${\displaystyle I_{y}\,\!(a,b)}$ は、正則化された不完全ベータ関数,

${\displaystyle y={\frac {x^{2}}{x^{2} \nu }},}$

${\displaystyle p_{j}={\frac {1}{j!}}\exp \left\{-{\frac {\mu ^{2}}{2}}\right\}\left({\frac {\mu ^{2}}{2}}\right)^{j},}$

${\displaystyle q_{j}={\frac {\mu }{{\sqrt {2}}\Gamma (j 3/2)}}\exp \left\{-{\frac {\mu ^{2}}{2}}\right\}\left({\frac {\mu ^{2}}{2}}\right)^{j},}$

であり、Φ は標準正規分布の累積分布関数である。

他の表現として、以下の書き方もできる。

${\displaystyle F_{v,\mu }(x)={\begin{cases}{\frac {1}{2}}\sum _{j=0}^{\infty }{\frac {1}{j!}}(-\mu {\sqrt {2}})^{j}e^{\frac {-\mu ^{2}}{2}}{\frac {\Gamma ({\frac {j 1}{2}})}{\sqrt {\pi }}}I\left({\frac {v}{v x^{2}}};{\frac {v}{2}},{\frac {j 1}{2}}\right),&x\geq 0\\1-{\frac {1}{2}}\sum _{j=0}^{\infty }{\frac {1}{j!}}(-\mu {\sqrt {2}})^{j}e^{\frac {-\mu ^{2}}{2}}{\frac {\Gamma ({\frac {j 1}{2}})}{\sqrt {\pi }}}I\left({\frac {v}{v x^{2}}};{\frac {v}{2}},{\frac {j 1}{2}}\right),&x<0\end{cases}}}$

ここで、Γ は ガンマ関数 、I は、正則化された不完全ベータ関数である。

確率密度関数

この非心t分布の確率密度関数は

${\displaystyle f(t)={\frac {\nu ^{\nu /2}e^{-\nu \mu ^{2}/2(t^{2} \nu )}}{{\sqrt {\pi }}\Gamma (\nu /2)2^{(\nu -1)/2}(t^{2} \nu )^{(\nu 1)/2}}}}$

${\displaystyle \times \int _{0}^{\infty }x^{\nu }\exp \left[-{\frac {1}{2}}\left(x-{\frac {\mu t}{\sqrt {t^{2} \nu }}}\right)^{2}\right]\,dx}$

ここで ν > 0 である。この確率密度関数の定義域は実数である。

非心t分布の平均および分散は

${\displaystyle \operatorname {E} \left[T\right]={\begin{cases}\mu {\sqrt {\frac {\nu }{2}}}{\frac {\Gamma ((\nu -1)/2)}{\Gamma (\nu /2)}}&\nu >1\\{\mbox{Does not exist}}&\nu \leq 1\end{cases}}}$

${\displaystyle \operatorname {Var} \left[T\right]={\begin{cases}{\frac {\nu (1 \mu ^{2})}{\nu -2}}-{\frac {\mu ^{2}\nu }{2}}\left({\frac {\Gamma ((\nu -1)/2)}{\Gamma (\nu /2)}}\right)^{2}&\nu >2\\{\mbox{Does not exist}}&\nu \leq 2\end{cases}}.}$

特別の場合

もしも μ = 0 の場合、非心t分布はt分布になる。

関連する分布

• もしも T が非心t分布にしたがう場合、Z = T² とおくと Z は非心F分布にしたがう。
• T が非心t分布にしたがう場合、${\displaystyle Z=\lim _{\nu \to \infty }T}$ とおくと、Z は正規分布にしたがう。

関連事項

• カイ二乗分布
• 非心F分布
• 正規分布
• t分布

出典

外部リンク

• Eric W. Weisstein. "Noncentral Student's t-Distribution." From MathWorld--A Wolfram Web Resource

翻訳元

本記事は英語版ウィキペディア記事

• Noncentral chi-square_distribution. [:en] Wikipedia: Free Encyclopedia (English language), 14:14, 21 July 2007

からの抄訳に基づいて作成された。