頂点推移グラフ

数学のグラフ理論の分野における頂点推移グラフ（ちょうてんすいいグラフ、英: vertex-transitive graph）とは、与えられた任意の二頂点 v₁ および v₂ に対して

f(v_{1})=v_{2}\

であるような自己同型

f:V(G)\rightarrow V(G)\

が存在するグラフ G のことを言う。

言い換えれば、グラフが頂点推移的であるとは、その自己同型群が各頂点の上で可移的（transitively）に作用することを言う。グラフが頂点推移的であるための必要十分条件は、その補グラフが頂点推移的であることである（なぜならば、それらの群作用は等しいため）。

孤立頂点を含まない対称グラフは、頂点推移的である。また、頂点推移グラフは正則である。しかし、すべての頂点推移グラフが対称であるとは限らない（例えば、切頂四面体の辺から成るグラフ）。また、すべての正則グラフが頂点推移的であるとは限らない（例えば、フルフトグラフ）。

有限の例

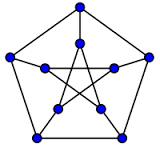
対称グラフ（例えば、ピーターセングラフ、ヒーウッドグラフ、正多面体の頂点と辺から成るグラフなど）であれば、有限の頂点推移グラフである。有限のケイリーグラフ（例えば、キューブ連結サイクルなど）もまた、頂点推移的である。なぜならば、それは半正多面体の頂点と辺から成るため（それらのうち対称であるものは二つしかないが）である。Potočnik、Spiga および Verret は、最大 1280 個の頂点を含む全ての連結立体頂点推移グラフの調査を行った。

性質

頂点推移グラフの辺連結度は、その次数 d に等しい。一方、その頂点連結度は少なくとも 2(d 1)/3 である。そのグラフの次数が 4 以下であるか、グラフが辺推移的であるか、あるいは最小のケイリーグラフであるなら、その頂点連結度も次数 d と等しくなる。

無限の例

無限な頂点推移グラフは次を含む:

無限路（両方向に無限）
無限正則木。例えば、自由群のケイリーグラフ
正多角形によるタイル張りを含む、平面一様充填のグラフ（平面充填の一覧を参照されたい）
無限ケイリーグラフ
ラドグラフ

二つの可算な頂点推移グラフが準等距離同型（quasi-isometric）であるとは、それらの距離函数の比が上下ともに有界であることを言う。有名な予想に、全ての無限な頂点推移グラフはケイリーグラフと準等距離同型である、というものがあったが、その反例はディエステルとリーダーによって提唱され、近年、エスキン、フィッシャーおよびホワイトによってその確証が得られた。