扇形

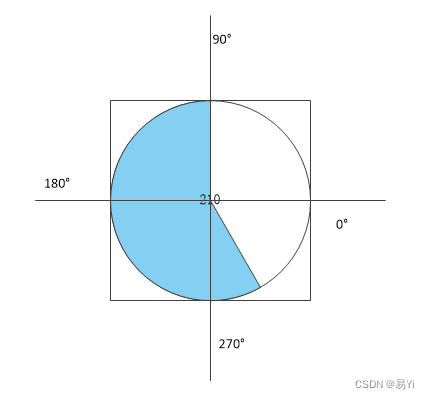
扇形（おうぎがた、英: circular sector）は、平面図形の一つで、円の2本の半径とその間にある円弧によって囲まれた図形である。

数学的な記述

2本の半径がなす角を扇形の中心角という。中心角が 180° のものは半円であり、円は中心角 360° の扇形と考えることもできる。

円Oから、２本の半径OA,OBが切り取る扇形を扇形O-⌒ABと呼ぶ（⌒はABの上にかぶせて書くのが正しい）。

円を異なる2本の半径で分割すると必ず2つの扇形ができ、それらの中心角の和は 360° である。

扇形の円弧（曲線部分）の長さ l は中心角の大きさに比例する。

半径 r の円の円周の長さは 2πr であるので、中心角が θ の扇形の円弧の長さは

l=2\pi r\times {\frac {\theta }{2\pi }}=r\theta

となる。

同様に扇形の面積 S も中心角の大きさに比例する。

半径 r の円板の面積は πr² であるので、中心角が θ のとき

S=\pi r^{2}\times {\frac {\theta }{2\pi }}={\frac {1}{2}}r^{2}\theta

となる。また θ = l/r より

S={\frac {1}{2}}rl

となる。

円錐の展開図では側面にあたる部分は扇形になる。